Como achar o valor de a na função afim?
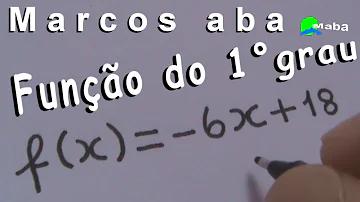
Como achar o valor de a na função afim?
Coeficientes da Função Afim Em f(x)= ax +b, o valor de a é identificado como taxa de variação (crescimento) ou de coeficiente angular porque aponta o quanto a função pode crescer e a inclinação da reta em relação ao eixo da abscissa (x) no plano cartesiano.
O que é o valor Numerico de uma função?
O “valor numérico” diz respeito ao valor obtido quando analisamos uma função polinomial (ou polinômio), com um determinado valor para a variável x. Assim sendo, considere um polinômio p(x) e um número real λ.
Como descobrir o valor de aeb em uma equação?
Para achar a e b na função afim devemos encontrar pelo menos dois pontos (x,y) que correspondem as condições de contorno do modelo. Em seguida, é preciso substituir os valores na função e montar um sistema de equações que, ao ser resolvido, mostrará os valores de a e b da função afim.
Quais os coeficientes da função afim?
Os coeficientes da função afim Vamos determinar a função que passa por dois pontos. Para isso, precisamos encontrar as coordenadas destes dois pontos, sendo que a coordenada y’ é determinada pelo valor da função na coordenada x’ (x1, f (x1)), (x2, f (x2)).
Como identificar se a função afim é crescente ou decrescente?
Para identificar se uma função afim é crescente ou decrescente, basta verificar o valor do seu coeficiente angular. Se o coeficiente angular for positivo, ou seja, a é maior que zero, a função será crescente. Ao contrário, se a for negativo, a função será decrescente. Por exemplo, a função 2x - 4 é crescente, pois a = 2 (valor positivo).
Qual é o valor mínimo da função?
Esse é o valor mínimo da função, pois a parábola se abre para cima. . Esse é o valor máximo da função, porque a parábola se abre para baixo. Determine o vértice. Se forem pedidas as coordenadas do valor máximo ou mínimo, o ponto será . No entanto, observe que, na forma padrão, o termo da equação que fica entre parênteses será .
Como calcular a função?
Se f (1)=-9 e b²-a²=54, calcule o valor de a-b. Para resolver esse exercício, temos que ter em mente os produtos notáveis, mas antes vamos à parte que envolve a função. Vamos escrever a função, conforme passado pelo exercício. Pronto, esse é a parte que envolvia função, somente montar a função.














