O que é uma distribuição continua?

O que é uma distribuição continua?
A distribuição contínua descreve as probabilidades dos possíveis valores de uma variável aleatória contínua. Uma variável aleatória contínua é uma variável aleatória com um conjunto de valores possíveis (conhecidos como a intervalos) que é infinito e incontável.
Qual é o conceito de variável aleatória?
Variáveis Aleatórias É o tipo de variável que assume um número finito de valores possíveis ou número infinito enumerável. De um modo geral, os valores de X pertencem ao conjunto dos inteiros.
Qual a probabilidade de uma variável aleatória contínua?
As probabilidades de variáveis aleatórias contínuas (X) são definidas como a área sob a curva da sua distribuição. Assim, apenas as faixas de valores podem ter uma probabilidade diferente de zero. A probabilidade de que uma variável aleatória contínua seja igual a algum valor é sempre zero. Exemplo da distribuição de pesos
Qual a variável aleatória?
Em outras palavras, a variável aleatória traduz o resultado do experimento em números reais. No cálculo de probabilidades, estudam-se as V.A.s (Variáveis Aleatórias) e calculam-se as probabilidades associadas a elas. Uma medida de probabilidade é associada ao espaço amostral por meio de uma variável aleatória X.
Qual a corrente das variáveis aleatórias?
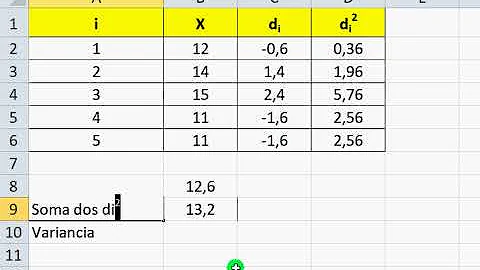
Variáveis Aleatórias Contínuas Distribuições e Função Densidade Funções de Distribuição Cumulativa Média e Variância de uma variável contínua Porém se dizemos que a corrente é 14,47 miliampéres esse valor é arredondado. A corrente está na verdade na faixa [14,465 ≤ x ≤ 14,475].
Quais são as variáveis aleatórias e distribuição de probabilidades?
Variáveis Aleatórias Contínuas e Distribuição de Probabilidades - parte I Variáveis Aleatórias Contínuas Distribuições e Função Densidade Funções de Distribuição Cumulativa Média e Variância de uma variável contínua Variáveis Aleatórias Contínuas e Distribuição de Probabilidades - parte I