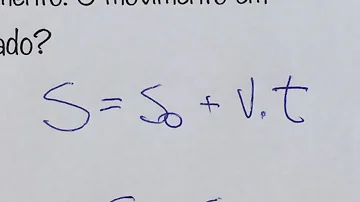Como identificar a raiz de um gráfico?

Como identificar a raiz de um gráfico?
Para determinarmos o zero ou a raiz de uma função basta considerarmos f(x) = 0 ou y = 0. Raiz ou zero da função é o instante em que a reta corta o eixo x.
O que é a raiz de um gráfico?
Calcular o valor da raiz da função é determinar o valor em que a reta cruza o eixo x, para isso consideremos o valor de y igual a zero, pois no momento em que a reta intersecta o eixo x, y = 0. ... Portanto, para calcularmos a raiz de uma função do 1º grau, basta utilizar a expressão x = x = –b/a.
Como obter a raiz quadrada de um número negativo?
Você não pode obter a raiz quadrada de um número negativo; por isso, qualquer valor x que resulte em um número negativo deve ser excluído do domínio dessa função. Por exemplo: identifique o domínio da função f (x) = √ (x + 3). Os termos dentro do radical são (x + 3). Torne-os maiores ou iguais a zero: (x + 3) ≥ 0.
Como construir um gráfico do 1o grau?
Na construção de um gráfico de uma função do 1º grau basta indicar apenas dois valores pra x, pois o gráfico é uma reta e uma reta é formada por, no mínimo, 2 pontos. Apenas um ponto corta o eixo x, e esse ponto é a raiz da função. Apenas um ponto corta o eixo y, esse ponto é o valor de b.
Qual o gráfico de função do 1o grau?
Gráfico de Função do 1º grau. Gráfico de função do 1º Grau Ouvir: Gráfico de Função do 1º grau. Gráfico de função do 1º Grau Toda função pode ser representada graficamente, e a função do 1º grau é formada por uma reta. Essa reta pode ser crescente ou decrescente, dependendo do sinal de a. Isso significa que a será positivo.
Qual a propriedade do produto das raízes?
Nesse caso, como o produto entre duas raízes é zero, temos pela propriedade do produto das raízes, que: x – 2 = 0 ou 2 x -1 = 0. Assim, as raízes reais do polinômio são os pontos (2, 0) e (1/2, 0). Importante: funções polinomiais podem ter raízes reais e imaginárias.