Como se determina a lei da função?

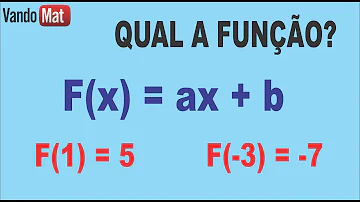
Como se determina a lei da função?

Toda função é definida por uma lei de formação, no caso de uma função do 1º grau a lei de formação será a seguinte: y = ax + b, onde a e b são números reais e a ≠ 0. Esse tipo de função deve ser dos Reais para os Reais.

Como verificar a identidade de uma função?

A função identidade, também nomeada de função inclusão, é uma das categorias da função afim (f(x) = ax + b). Os valores do seu domínio são os mesmos da imagem do contradomínio. Por isso, a função identidade é também bijetora, isto é, para qualquer valor que seja x o resultado da sua função será ele mesmo (f(x) = x).

Como descobrir o valor de F?

Uma função f é dada por f(x) = ax + b, em que a e b são números reais. Considerando que f(–1) = 3 e f(1) = –1, determine f(3). Determinando a função de acordo com f(x) = ax + b → f(x) = –2x + 1. O valor de f(3) na equação é igual a –5.

Como calcular o limite de uma função?

Vamos determinar o limite da função f(x) = x² – 5x + 3, quando x tende a 4. Nesse caso devemos aplicar a seguinte regra: o limite das somas é a soma dos limites. Portanto, devemos determinar o limite de cada monômio e depois realizar a soma entre eles.

O que é função identidade exemplos?

Neste caso, o seu gráfico será uma reta paralela ao eixo Ox. Ao passo que, quando b = 0 e a = 1 a função é chamada de função identidade. O gráfico da função f (x) = x (função identidade) é uma reta que passa pela origem (0,0). ... Por exemplo as funções f (x) = 2x e g (x) = - 3x são funções lineares.

Quais são os valores da função afim?

Os valores de f (0), f (2), f (-1) e f (5), são, respectivamente: Uma função do 1º grau é dada por f (x) = ax + b. Sabe-se que f (1) = 5 e f (-3) = -7. Essa função é: Depois desses exercícios, você já está pronto para encarar os problemas mais elaborados sobre função afim, como os que são propostos no Enem e nos vestibulares.

Será que as funções afim não têm nada a ver com afinidade?

Não, não. Funções afim não têm nada a ver com afinidade, não foi dessa vez hahaha Nós sempre vamos pensar nas funções com aquela definição que vimos antes: TODO elemento do domínio se relaciona a um ÚNICO elemento do contradomínio. Show! Mas a forma como essas relações acontecem, aparece de forma diferente, ou seja, tem LEIS DE FORMAÇÃO diferente.

Como identificar se a função afim é crescente ou decrescente?

Para identificar se uma função afim é crescente ou decrescente, basta verificar o valor do seu coeficiente angular. Se o coeficiente angular for positivo, ou seja, a é maior que zero, a função será crescente. Ao contrário, se a for negativo, a função será decrescente. Por exemplo, a função 2x - 4 é crescente, pois a = 2 (valor positivo).