Como identificar as funções exponenciais?

Como identificar as funções exponenciais?

Tipos de função exponencial O gráfico da função f(x) = ax é crescente quando a base é um número maior do que 1, ou seja, quando a > 1. Nesse caso, quanto maior o valor de x maior será o valor de y. A função exponencial é decrescente quando a base é um número maior que 0 e menor que 1, ou seja, quando 0

Como resolver uma equação exponencial?

Uma função exponencial é uma função que possui uma variável como expoente. Matematicamente, ela pode ser representada por f de R em R, que é obtida pela lei de formação f(x) = ax, em que “a” é um número real dado, a > 0 e a ≠ 1.

Quais as áreas de conhecimento que fazem uso das funções exponenciais?

As funções exponenciais possuem uma diversidade de aplicações do cotidiano, estão presentes em diversas ciências como: na Matemática financeira é utilizada na capitalização de capitais pelo método do juro composto, na Geografia está relacionada a expressões responsáveis por explicar os crescimentos populacionais, na ...

Como identificar uma função logarítmica?

A função logarítmica é dada pela lei f(x) = logax, no qual "a" é a base positiva (a > 0) e sempre diferente de 1. Nesse tipo de função, o logaritmo de base "a'', ligado a determinado valor de b, tem o expoente igual a x, que é a potência da base que resulta justamente em b.

O que são funções exponenciais e logarítmicas?

A função exponencial é aquela em que a variável está no expoente, e a base é sempre maior do que 0 e diferente de 1. ... A inversa da função exponencial é a chamada função logarítmica. Ela é definida basicamente como f(x) = log ax, em que a é um número real positivo e diferente de 1.

Como igualar o expoente?

Quando as bases são iguais, pela propriedade de igualdade de potência, os expoentes são iguais. Igualando-se os expoentes, basta resolver a equação polinomial. Realizando a fatoração de 625, sabemos que 625 = 54.

Qual o valor de exponencial?

2,718281828 A função exponencial natural, denotada ex ou exp(x) é a função exponencial cuja base é o número de Euler (um número irracional que vale aproximadamente 2,718281828). A exponencial natural é caracterizada por ser idêntica à sua própria derivada.

Quais são os tipos de funções exponenciais?

As funções exponenciais, assim como as funções normais, podem ser classificadas como crescentes ou decrescentes, dependendo de a base a ser maior ou menor que 1.

Quais as principais aplicações das funções exponencial é logarítmica?

A função logarítmica, assim como sua inversa, a função exponencial, são instrumentos para relatar matematicamente a evolução de grandezas, nas quais o crescimento ou decrescimento são proporcionais à quantidade dessa grandeza em um determinado tempo.

Quando a função exponencial é decrescente?

A função exponencial é decrescente quando a base é um número maior que 0 e menor que 1, ou seja, quando 0<1. Caso ela seja decrescente, quanto maior o valor de x menor será o valor de y. Veja também: Tipos de gráficos – quando usar cada um?

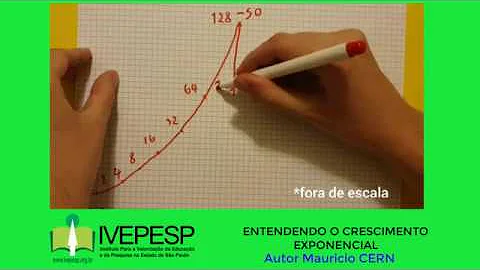
Como ocorre o crescimento exponencial?

Crescimento exponencial. A função exponencial aparece na forma f (x)=aX, sendo a um número real, maior que zero e diferente de um. E o crescimento exponencial é aquele que por um período sofre a multiplicação por uma constante, que inicia de forma gradual, mas que se acentua rapidamente. Veja como ficaria graficamente:

Qual a definição de crescimento e decrescimento de funções?

Definição de crescimento e decrescimento de funções Seja a função e dois pontos do domínio , então dizemos que. A função é crescente nos intervalos onde ; A função é decrescente nos intervalos onde ; A função é constante nos intervalos onde . Agora relembre a definição de derivada para cada ponto do domínio.

Como determinar se a função é decrescente?

Se a < 0, a função é decrescente. Vamos determinar se as funções a seguir são crescentes ou decrescentes. Crescente, pois a = 2 > 0. Decrescente, pois a = – 1 < 0. Decrescente, pois a = – 4 < 0. Crescente, pois a = 4 > 0. Quando uma função não é crescente nem decrescente, ou seja, quando a = 0, ela é uma função constante.