Como resolver continhas de divisões?
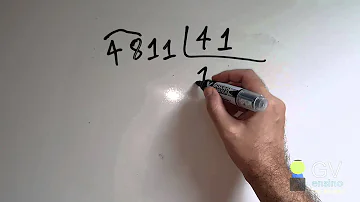
Como resolver continhas de divisões?
Onde 20 é chamado dividendo, 4 é divisor e 5, que é o resultado da conta de dividir, é denominado quociente. Observe que 20:4 = 5 pode ser justificado usando a multiplicação 4·5 = 20. Isso acontece porque multiplicação e divisão são operações inversas.
Qual é a ideia da divisão?
Para realizar uma divisão, devemos utilizar o chamado algoritmo de Euclides, ou seja, devemos imaginar um número (quociente) que, quando multiplicado com o divisor, seja igual ou se aproxime o máximo possível do dividendo. Caso você encontre um número cuja multiplicação seja igual ao dividendo, a divisão chega ao fim.
Qual o critério de divisibilidade em divisões?
O caso mais especial em que o uso de critérios de divisibilidade em divisões é importante é aquele no qual precisamos encontrar mínimo múltiplo comum, máximo divisor comum ou apenas a decomposição em fatores primos de um número. Esse último pode ser usado para facilitar cálculos envolvendo diversos saberes, inclusive cálculo de raízes.
Como fazer a divisão de dividendo e divisor?
Para realizar a divisão, vamos escrever o número 30 na forma 30,0. Agora que o dividendo e o divisor têm um número após a vírgula, podemos desconsiderar as vírgulas e realizar a divisão entre 300 e 25, obtendo como resultado o quociente 12, como podemos ver na figura a seguir.
Como dividir o resto da divisão?
Passo 3 – Agora devemos dividir o resto da divisão pelo divisor, ou seja, dividir o número 1 por 2. Mas como o número 1 não é divisível por 2, devemos acrescentar uma vírgula no quociente e acrescentar um zero no resto. Passo 4 – Agora continuamos a divisão normalmente.
Como facilitar o processo de divisão?
Para facilitar o processo de divisão, temos um algoritmo, isto é, temos um passo a passo que pode facilitar. Para verificarmos esse processo, vamos tomar a seguinte divisão 64: 4. Primeiro passo: montar a operação utilizando o método da chave. Segundo passo: tentar encontrar um número que multiplicado por 4 seja igual a 64.