Qual a definição de uma função do 1º grau?
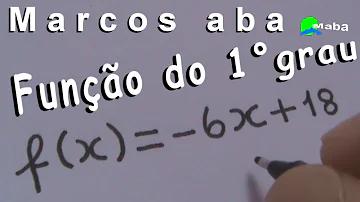
Qual a definição de uma função do 1º grau?
A função de primeiro grau ou função afim é uma norma matemática que relaciona as variáveis de uma equação, ou seja, a dependência de um elemento em relação ao outro. Por isso, a função de primeiro grau é utilizada para definir a relação entre as variáveis x e y. Isso porque para cada valor dado a x, determinará o de y.
Como calcular uma função de primeiro grau?
A formação de uma função do 1º grau é expressa da seguinte forma: y = ax + b, onde a e b são números reais e a é diferente de 0. Consideremos x e y duas variáveis, sendo uma dependente da outra, isto é, para cada valor atribuído a x corresponde um valor para y.
Por que essa função não é do primeiro grau?
Essa função não é do primeiro grau porque a variável independente possui grau 2. Nesse caso, ela é uma função do segundo grau. b) y = 1/x. Essa função não é do primeiro grau porque y = 1/x também pode ser escrito como y = x -1 e esse (-1) não é o expoente correto para as funções do primeiro grau.
Como calcular a função de 1o grau?
Aprenda como calcular a função de 1º grau e pratique com muitos exercícios! Muito conhecida pelos estudantes e constantemente sendo cobrada nos vestibulares, a função de 1º grau é uma matéria importantíssima na Matemática. Isso porque, para entender as outras funções mais complexas (de 2º grau, exponencial e logarítmica, por exemplo), é preciso ...
Como resolver uma equação do primeiro grau?
De posse dessas definições, seguem os quatro passos para resolver uma equação do primeiro grau. Os quatro passos da resolução de equações do primeiro grau. Passo 1 – Colocar no primeiro membro todos os termos que possuem incógnita. Reescreva a equação colocando todos os termos que possuem incógnita no primeiro membro.
Qual a função do 2° grau?
Gráfico de uma função do 1° grau. If playback doesn't begin shortly, try restarting your device. If playback doesn't begin shortly, try restarting your device. Determine a função afim f (x) = ax + b, sabendo que f (1) = 5 e f (–3) = –7. Seja a função f de R em R definida por f (x) = 54x + 45, determine o valor de f (2 541) – f (2 540).














