Como fazer cálculo com vetores?
Índice
- Como fazer cálculo com vetores?
- Como se calcula o módulo de um vetor?
- Como calcular o módulo do vetor diferença?
- Como calcular a resultante de um vetor?
- Como calcular o vetor força resultante?
- Como multiplicar um vetor por um número real?
- Qual o vetor utilizado para o Plano Z?
- Como devemos desenhar os dois vetores?
- Quais são os vetores unitários?
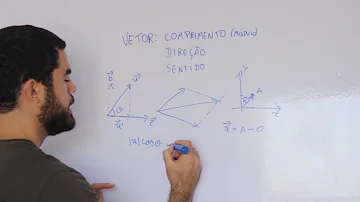
Como fazer cálculo com vetores?
u = P – O = (x, y) – (0, 0) = (x – 0, y – 0 ) = (x, y). Logo, o vetor u, fica expresso através de um par ordenado, referido à origem do sistema de coordenadas cartesianas.
Como se calcula o módulo de um vetor?
Módulo ou norma de um vetor
- Módulo ou norma de um vetor. ...
- Como esse vetor possui apenas duas coordenadas e, portanto, pertence ao plano bidimensional, utiliza-se a distância entre dois pontos do plano para calcular seu comprimento. ...
- |v| = √(a2 + b2)
Como calcular o módulo do vetor diferença?
Portanto, o módulo entre dois números reais x e y fica definido como o valor absoluto da diferença entre x e y e é denotado por |x – y|. Dessa forma, o módulo representa a distância entre dois números reais na reta numérica.
Como calcular a resultante de um vetor?
Quando temos diversos vetores e queremos encontrar o vetor resultante, devemos conectá-los uns aos outros. Nesse processo, que independe da ordem escolhida, devemos ligar a ponta de um vetor ao início do próximo.
Como calcular o vetor força resultante?
Para encontrar a força resultante, nós precisaremos decompor os dois vetores, somar suas componentes e então calcular o módulo do vetor resultante.
Como multiplicar um vetor por um número real?
Quando multiplicamos um vetor por um número real a sua direção não é alterada. Entretanto, o seu sentido e o seu módulo podem ser alterados. . Se multiplicarmos por , mas o comprimento é o dobro. . Para a base cartesiana, teríamos:
Qual o vetor utilizado para o Plano Z?
Caso o problema a ser resolvido seja dado em três dimensões, o vetor utilizado para o plano z é o vetor unitário . Então, a projeção do vetor no eixo x do plano cartesiano será dado por , e sua projeção no eixo y do plano será: . Este vetor pode ser escrito como:
Como devemos desenhar os dois vetores?
O exercício nos deu o desenho dos dois vetores que devemos considerar. Com esse desenho devemos realizar operações entre vetores. Aqui, como foi nos pedido devemos desenhar os vetores. no sentido oposto. . Primeiro, vamos encontrar os vetores para soma :
Quais são os vetores unitários?
Quaisquer que sejam k e c escalares, v e w vetores: O módulo ou comprimento do vetor v= (a,b) é um número real não negativo, definido por: Vetor unitário é o que tem o módulo igual a 1. Existem dois vetores unitários que formam a base canônica para o espaço R², que são dados por:












