Como calcular distância focal da hipérbole?
Como calcular distância focal da hipérbole?
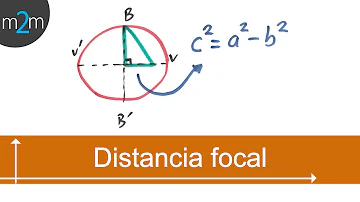
Elementos e propriedades da hipérbole: 2c → é a distância focal. c2 = a2 + b2 → relação fundamental. A1(– a, 0) e A2(a, 0) → são os vértices da hipérbole.
Como é calculada a excentricidade da hipérbole?
O quociente c/a é conhecido como excentricidade da hipérbole. Como, por definição, a < c, concluímos que a excentricidade de uma hipérbole é um número positivo maior que a unidade. O ponto (0,0) é o centro da hipérbole. Observe que x – (-c) = x + c.
Como se calcula a área de uma elipse?
A área da elipse é a x b x π. Como você está multiplicando duas unidades de medida, a resposta estará em unidades quadradas. Por exemplo, se uma elipse tem um raio menor de 3 unidades e um raio maior de 5 unidades, a área será igual a 3 x 5 x π, que é aproximadamente 47 unidades quadradas.
Como calcular a distancia entre os focos da elipse?
SOLUÇÃO: a elipse é a do problema anterior. Portanto a distancia focal ou seja, a distancia entre os focos da elipse será: D = 4 – (- 4) = 8 u.c (u.c. = unidades de comprimento). 4 – Calcular a distancia focal e a excentricidade da elipse 25x y .
Qual é a circunferência da elipse?
Perímetro ou circunferência : comprimento total da curva da elipse. Área : área da elipse; . Excentricidade : uma medida de quão perto está da curva de um círculo; . Distância focal: distância entre os focos da elipse; . Proporção Y / X , Eixo menor / Eixo maior : relação entre os dois eixos. Uma medida de excentricidade.
Quais são os focos da elipse?
Na equação, quando a > b, então os focos da elipse estarão sobre o eixo x e teremos que: a² = b² + c², em que 2c é a distância focal, como vimos anteriormente.
Como desenvolver a equação da elipse?
Na geometria analítica, é bastante comum buscar descrever figuras geométricas por meio da álgebra. Sendo assim com os estudos dessa cônica, foi possível desenvolver-se a equação da elipse com centro na origem: Na equação, quando a > b, então os focos da elipse estarão sobre o eixo x e teremos que:














