Como calcular um função?
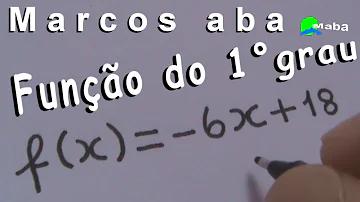
Como calcular um função?
Toda função é definida por uma lei de formação, no caso de uma função do 1º grau a lei de formação será a seguinte: y = ax + b, onde a e b são números reais e a ≠ 0. Esse tipo de função deve ser dos Reais para os Reais.
Quais dessas funções são funções afins?
A função afim, também chamada de função do 1º grau, é uma função f : ℝ→ℝ, definida como f(x) = ax + b, sendo a e b números reais. As funções f(x) = x + 5, g(x) = 3√3x - 8 e h(x) = 1/2 x são exemplos de funções afim.
Para que serve a função FX no Excel?
2) Na barra de ferramentas do Excel existe o botão fx, que serve para chamarmos as funções já implementadas no excel. Aperte este botão e, no meio das diversas funções definidas pelo usuário, selecione a função "MinhaFuncao" clicando duas vezes sobre o nome da função.
Como calcular a função de 1o grau?
Aprenda como calcular a função de 1º grau e pratique com muitos exercícios! Muito conhecida pelos estudantes e constantemente sendo cobrada nos vestibulares, a função de 1º grau é uma matéria importantíssima na Matemática. Isso porque, para entender as outras funções mais complexas (de 2º grau, exponencial e logarítmica, por exemplo), é preciso ...
Como encontrar a fórmula da função inversa de uma função?
Aprenda a encontrar a fórmula da função inversa de uma função dada. Por exemplo, encontre a inversa de f (x)=3x+2. Funções inversas, no sentido geral, são funções que "revertem" umas as outras. Por exemplo, se .
Como calcular a raiz de uma função?
1 – Sabendo que a função f (x)=mx+n admite 5 como raiz e f (-2)=-63, calcule o valor de f (16). Quando falamos em raiz de uma função quer dizer que f (x)=0, portanto o enunciado nos informa que f (5)=0. O exercício nos forneceu outra informação importante, do qual poderemos isolar uma incógnita e montar um sistema.
Como calcular a função decrescente?
Para o estudo da função decrescente, a análise é reversa, isto é, se aumentamos o “x”, o valor de “y” decresce. Veja abaixo o exemplo: Considere a função: y = – 2x + 1. Se x = 1, ao substituirmos, achamos y = – 1. Adotando o mesmo raciocínio, se x = 2, y = – 3. Por fim, se x = 3, y = – 5.














