Como interpretar uma regressão linear simples?

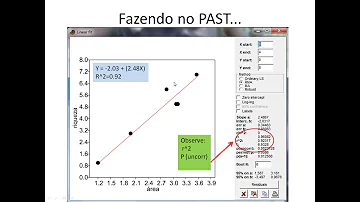
Como interpretar uma regressão linear simples?

Na regressão linear simples, a relação entre duas variáveis pode ser representada por uma linha reta, criando uma relação direta de causa e efeito. Assim, será possível prever os valores de uma variável dependente com base nos resultados da variável independente, como ocorre num gráfico de uma equação de primeiro grau.

Como fazer análise de regressão múltipla?

Muitas vezes uma única variável explicativa (preditora) não será capaz de explicar tudo a respeito da variável resposta. Se em vez de uma, forem incorporadas várias variáveis independentes, passa-se a ter uma análise de regressão linear múltipla. Y é a variável dependente (resposta);

O que é análise de regressão linear?

A regressão linear múltipla é uma técnica estatística responsável pela análise de situações envolvendo mais de uma variável. Esse método nos permite identificar quais são as variáveis independentes que podem explicar uma variável independente, comprovar as causas e prever os valores aproximados.

Quando fazer uma análise de regressão?

A análise de regressão é útil para uma organização, pois permite determinar o grau em que as variáveis independentes influenciam as variáveis dependentes. Além disso, permite explicar um fenômeno e prever coisas sobre o futuro, assim como também pode obter informações comerciais valiosas e acionáveis.

Por que a análise de regressão é uma possibilidade?

É importante notar que, apesar de ser uma possibilidade, a análise de regressão não tem como objetivo obter estimativas pontuais de eventos futuros, mas sim de estimar médias condicionais e efeitos.

Qual o modelo linear de 1o grau?

MODELO LINEAR DE 1º GRAU (Regressão Linear Simples) O modelo estatístico para esta situação seria: Yi =β0 +β1Xi+ei em que: Yi= valor observado para a variável dependente Y no i-ésimo nível da variável independente X. β0= constante de regressão. Representa o intercepto da reta com o eixo dos Y. β1= coeficiente de regressão.

Qual o coeficiente de regressão?

Representa o intercepto da reta com o eixo dos Y. β1= coeficiente de regressão. Representa a variação de Y em função da variação de uma unidade da variável X.

Como ocorre a regressão do fenômeno?

Isto acontece, devido ao fato do fenômeno que está em estudo, não ser um fenômeno matemático e sim um fenômeno que está sujeito a influências que acontecem ao acaso. Assim, o objetivo da regressão é obter um modelo matemático que melhor se ajuste aos valores observados de Y em função da variação dos níveis da variável X.